Destroy Transportation system
Time Limit
1s
Memory Limit
32768KB
Judge Program
Standard
Ratio(Solve/Submit)
66.67%(2/3)
Description:
Tom is a commander, his task is destroying his enemy’s transportation system.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
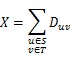
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
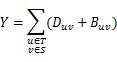
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
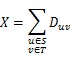
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
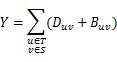
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Input:
There are multiply test cases.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
Output:
For each case, output "Case #X: " first, X is the case number starting from 1.If such set doesn’t exist, print “happy”, else print “unhappy”.
Sample Input:
2 3 3 1 2 2 2 2 3 2 2 3 1 2 2 3 3 1 2 10 2 2 3 2 2 3 1 2 2
Sample Output:
Case #1: happy Case #2: unhappy
Hint:
In first sample, for any set S, X=2, Y=4. In second sample. S= {1}, T= {2, 3}, X=10, Y=4.
Submit
