Decoding Morse Sequences
Before the digital age, the most common "binary" code for radio communication was the Morse code. In Morse code, symbols are encoded as sequences of short and long pulses (called dots and dashes respectively). The following table reproduces the Morse code for the alphabet, where dots and dashes are represented as ASCII characters "." and "-":
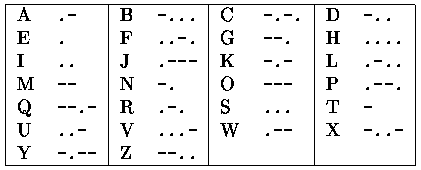
Notice that in the absence of pauses between letters there might be multiple interpretations of a Morse sequence. For example, the sequence -.-..-- could be decoded both as CAT or NXT (among others). A human Morse operator would use other context information (such as a language dictionary) to decide the appropriate decoding. But even provided with such dictionary one can obtain multiple phrases from a single Morse sequence.
Task
Write a program which for each data set:
reads a Morse sequence and a list of words (a dictionary),
computes the number of distinct phrases that can be obtained from the given Morse sequence using words from the dictionary,
writes the result.
Notice that we are interested in full matches, i.e. the complete Morse sequence must be matched to words in the dictionary.
The first line of the input contains exactly one positive integer d equal to the number of data sets, 1 <= d <= 20. The data sets follow.
The first line of each data set contains a Morse sequence - a nonempty sequence of at most 10 000 characters "." and "-" with no spaces in between.
The second line contains exactly one integer n, 1 <= n <= 10 000, equal to the number of words in a dictionary. Each of the following n lines contains one dictionary word - a nonempty sequence of at most 20 capital letters from "A" to "Z". No word occurs in the dictionary more than once.
The output should consist of exactly d lines, one line for each data set. Line i should contain one integer equal to the number of distinct phrases into which the Morse sequence from the i-th data set can be parsed. You may assume that this number is at most 2 * 10^9 for every single data set.
1 .---.--.-.-.-.---...-.---. 6 AT TACK TICK ATTACK DAWN DUSK
2
Submit
