Cube
After many years of development, Merck has finally discovered a simple model which helps with computer aided drug design. Different chemical substances are viewed as two-dimensional 損uzzle? pieces which may be combined in a three-dimensional way, forming more complex structures of atoms. Special combinations of these pieces have very special chemical properties. These combinations which are known as ACM (Anachronistic Cube Molecules) result from combining six individual puzzle pieces along their edges to form a complete cube (see Figure 3).
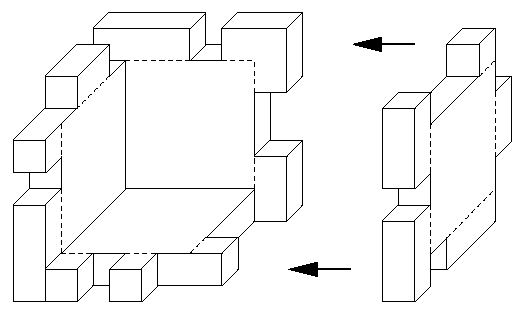
Given six pieces, decide whether they can be put together to form a cube of dimension 6 * 6 * 6, with no holes visible from the outside. Each piece can be thought of as being cut from a plate of wood of dimension 6 * 6 * 1, with the 4 * 4 * 1 plate in the centre untouched. A piece can be used the one or the other way around, i.e., there is no distinction between the inside and the outside.
The first line contains the number of scenarios.
In each scenario, you are first given six lines with a graphical representation of the six pieces. In that representation, "X" symbolises solid wood, a dot "." stands for a 1 * 1 * 1 piece of wood that was cut out. A column with "!" stands on the right of each piece to separate them from each other. There is a blank line following every scenario.
It is not necessary that the pieces can really be cut out of wood or that they form a stable cube, as you can see in the sample input, second example.
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. In the next line print "Yes" or "No" depending on whether the given pieces can be put together to form a cube. Terminate the output for the scenario with a blank line.
3 XX..XX!.X..X.!XX..XX!.X..X.!..XX..!..XX..! XXXXXX!.XXXX.!XXXXXX!.XXXX.!.XXXX.!.XXXX.! .XXXX.!XXXXXX!.XXXX.!XXXXXX!XXXXXX!XXXXXX! .XXXX.!XXXXXX!.XXXX.!XXXXXX!XXXXXX!XXXXXX! XXXXXX!.XXXX.!XXXXXX!.XXXX.!.XXXX.!.XXXX.! XX..XX!.X..X.!XX..XX!.X..X.!..XX..!..XX..! .XXXX.!.XXXX.!.XXXX.!.XXXX.!XXXXXX!X....X! XXXXXX!.XXXX.!XXXXXX!.XXXX.!XXXXXX!.XXXX.! XXXXXX!.XXXX.!XXXXXX!.XXXX.!XXXXXX!.XXXX.! XXXXXX!.XXXX.!XXXXXX!.XXXX.!XXXXXX!.XXXX.! XXXXXX!.XXXX.!XXXXXX!.XXXX.!XXXXXX!.XXXX.! ......!......!......!......!XXXXXX!X....X! ......!......!......!......!......!......! .XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.! .XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.! .XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.! .XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.!.XXXX.! ......!......!......!......!......!......!
Scenario #1: Yes Scenario #2: Yes Scenario #3: No
Submit
