Stacking Cubes

Consider the following pattern of positive integers:
3 3 1
3 1
2
Note that each row is left-justified and no longer than its preceding row. Also, the entries in each row,when read left to right, are non-increasing and the entries in each column, when read top to bottom are non-increasing. We will call such a pattern a stacking pattern (SP) because such a pattern can represent a way of stacking cubes in a corner in the following way: if you consider placing the topmost row and leftmost column against walls, then the SP gives a bird's-eye view of how many cubes are stacked vertically. The SP above represents the following corner stacking:

We will call the wall against the topmost row the right wall , and the wall against the leftmost column the left wall. Here is another SP and the corner stacking it represents:

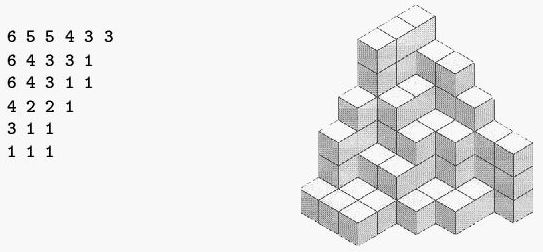
Note that if you rotate a corner stacking so the left wall becomes the floor and the floor becomes the right wall, you still have a corner stacking. (We will call this a left rotation.) Likewise, you would still have a corner stacking if you rotate so the right wall becomes the floor and the floor becomes the left wall. (We will call this a right rotation.) So the SP of the left and right rotations of the first SP given above are

3 2 1        3 3 2

2 1 1        2 1 1

2 1          1

You should check that both the left and right rotations of the second example SP are identical to the original SP.

This problem will consist of multiple problem instances. Each problem instance will consist of a positive integer n <= 11 indicating the number of rows in the SP that follows. (n = 0 indicates the end of input.)The rows of the SP will follow, one per line with entries separated by single spaces, delimited by a trailing 0. (The trailing 0 is, of course, not part of the input data proper and you may assume that each row given has at least one cube.) Each entry in the pattern proper will be a positive integer less than or equal to 20 and there will be no more than 20 entries in any row.

For each input SP you should produce two stacking patterns corresponding to the left rotation and the right rotation (in that order). Rows of the SP should be left-justified with entries separated by a single space. One blank line should separate the left and right rotations of the given SP and two blank lines should separate output for different problem instances.

3
3 3 1 0
3 1 0
2 0
6
6 5 5 4 3 3 0
6 4 3 3 1 0
6 4 3 1 1 0
4 2 2 1 0
3 1 1 0
1 1 1 0
0

3 2 1
2 1 1
2 1

3 3 2
2 1 1
1


6 5 5 4 3 3
6 4 3 3 1
6 4 3 1 1
4 2 2 1
3 1 1
1 1 1

6 5 5 4 3 3
6 4 3 3 1
6 4 3 1 1
4 2 2 1
3 1 1
1 1 1

Compiler C C++ Java Python2 Python3

Use advanced editor

Code