Shire
All the peoples living on Earth have decided that the hobbits, the keepers of the Ring of Power should be isolated in a region of the earth named Shire. The boundaries of the shire are represented by a convex polygon with a guard tower in each vertex.
The positions of all the towers from the region (two unsigned integers referring to a rectangular axis system) are given. A guard on a white horse is watching the shire's boundaries going over all the distances between two successive towers, one after the other, walking on a minimum way, only on paths parallel with the axis of the axis system.
The maximum length of the road that can be covered by the guard at a complete tour of the shire's boundaries is known and you are asked to determine a polygon with a maximum number of towers per outline, polygon that can be the boundary of the shire. Besides, the boundary has to contain the tower of Mordor (coordinates 0,0) on a vertex, in each of the other vertices being one of the existing towers.
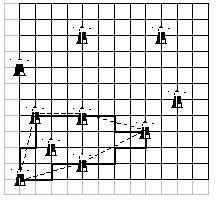
For example, for the towers location drawn in the figure above and for the 25 km limit of a tower made by a guard, the boundary of the shire can be made, in this order, from the towers of the following coordinates (0,0), (4,1), (8,3), (4,4), (1,4), (0,0). It can be observed that the polygon determined by these towers it's a convex polygon with 5 towers per outline.
The polygon with (0,0), (4,1), (4,12), (0,7), (0,0) has itself 5 towers per outline, but a complete tour of this polygon is over 25 km.
We should pay attention to the following observations:
• There can be towers strictly inside the polygon, but these are not taken into consideration for the maximum criterion;
• The degenerate polygon made only from one top (Mordor) or made from two towers (Mordor and another tower) or more collinear vertices it is considered a solution too;
• There can be collinear towers on the determined polygon's outline;
• In the input there are not two towers whose positions coincide and there is not a tower in the position (0,0).
The input has the fllowing structure:
N
x1 y1
x2 y2
...
xN yN
L
N is the number of towers in the shire (excepting the implicit tower – Mordor), (x1, y1) ... (xN, yN) are coordinates (abscise, ordinate) of each of the N towers, and L is number representing the maximum length of a complete tour of the polygon.
There are some restrictions:
• 0 < N <= 50
• 0 <= xi, yi <= 200
• 0 < L < 1000
The output will contain the number of towers on the polygon's outline.
9 0 7 1 4 2 2 4 1 4 4 4 9 8 3 9 9 10 5 25
5
Submit
